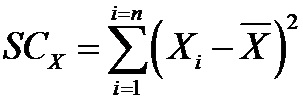
Se denomina comúnmente suma de cuadrados (SC) al numerador de la fórmula de la varianza. La suma de cuadrados de una muestra es la suma los cuadrados de las diferencias de cada valor de la muestra respecto de la media de esa muestra, esto es, a cada valor de la muestra se le resta el valor de la media de la muestra y esta diferencia se eleva al cuadrado. Al final se hace la suma de los cuadrados de estas diferencias. El procedimiento se expresa con la fórmula:

[1]

Este cálculo es muy común, y se puede realizar de varias maneras alternativas que proporcionan el mismo resultado. Una de estas alternativas es el uso de la fórmula

[2]

En ocasiones es válido preguntar si dos fórmulas son equivalentes, por lo que se hace necesario -y es a veces instructivo- observar el desarrollo de una fórmula para transformarla en una diferente que produzca el mismo resultado, pero que pueda ofrecer ventajas con respecto a la exactitud del cálculo o a la sencillez del procedimiento. Es por esto que presento aquí el desarrollo algebraico de la fórmula original [1] para transformarla en la fórmula [2] que reduce el error de redondeo, además de ser más sencilla en su ejecución al reducir el número de operaciones necesarias.

Como se observa en [1], el procedimiento consiste en sumar el valor de un binomio cuadrado, por lo que comenzaremos desarrollando el binomio como lo indica la fórmula [3]

[3]

Como siguiente paso, hay que considerar dos propiedades de la suma iterativa (SI).En primer lugar tenemos la propiedad distributiva que dice que
SI(a+b) = SI(a) + SI(b) , por lo que aplicamos esta propiedad a los tres términos en [4].

[4]

Después, hay que considerar que si sumamos n veces el valor de una constante K, el resultado es el mismo que se obtiene de multiplicar K por n. De modo que en [5] el 2 y la media, que son constantes, pasan a multiplicar la suma de X_i en el segundo término; y en el tercer término, si sumamos n veces el valor de la media podemos multiplicar el valor de n por el valor de la media.

[5]

Ahora podemos desglosar la fórmula de la media dividiendo la suma de valores de X entre el número de valores en el segundo término, y en el tercero también sin olvidar el paréntesis que obliga a dividir antes de elevar al cuadrado. El cambio de observa en [6].

[6]

Ahora, en el segundo término se multiplica el cociente que corresponde a la media por la suma de X_i, mientras que en el tercer término se elevan al cuadrado por separado el numerador y el denominador de la fórmula de la media

[7]

En [8], en el tercer término se multiplica n por la fracción que divide entre n². El resultado es la división del cuadrado de la suma de los valores de X entre el valor de n, dando como resultado que el primero y el segundo sean términos semejantes

[8]

Finalmente, al sumar algebraicamente los términos segundo y tercero llegamos a la fórmula [9] que es la misma que la fórmula [2]

[9]

Como resumen vamos a comparar los procedimientos indicados en ambas fórmulas.

De acuerdo con la fórmula [1], hay que calcular en primer lugar el valor de la media (sumar n números y dividir entre el número de valores), después se debe restar a cada número el valor de la media (n diferencias).El siguiente paso es elevar al cuadrado cada diferencia (n multiplicaciones) y sumar estos cuadrados (n operaciones).Finalmente, dividir esa suma entre el número de valores.

Esto significa que hay que realizar 4n operaciones más una que otra operación. A esto hay que agregar que cualquier error de redondeo obtenido en la media, será mayor entre mayor sea el número de operaciones realizadas.

Por otro lado, la fórmula [2] señala que se deben sumar los valores de X_i (n operaciones), se deben elevar al cuadrado los valores de X_i (n operaciones) y después sumarlos (n operaciones) finalmente dividir la suma de los valores de X_i elevados el cuadrado entre el número de valores y hacer la resta entre ambas sumas . En este caso, no solamente se reduce el número de operaciones necesarias, sino que solamente se realiza una división, por lo que se reduce considerablemente el error de redondeo en los cálculos. Por último, cabe decir que con este procedimiento el cálcula se puede implementar fácilmente en una hoja electrónica de cálculo lo cual simplifica su uso en procedimientos estadísticos más elaborados.