
Cuando se quiere describir un objeto -sea persona, animal o cosa-, siempre se hace considerando aquellas dimensiones que se considera relevantes. Por ejemplo, si es un animal su especie, su familia, su raza, el número de patas, el número de ojos, su color. Podríamos mencionar su peso en gramos, o toneladas, su estatura en milímetros o en metros, etcétera.
Se se tratase de una persona, podríamos mencionar su estatura, su peso, su sexo, su personalidad, qué tan simpático es, el color o largo de su cabello, qué tan guapo nos resulta o qué tan sensible es a los halagos inmerecidos.
Estas dimensiones se denominan variables. Podríamos definirlas como un conjunto de atributos o valores que nos pemiten distinguir entre objetos. Un punto importante aquí es que en nuestra descripción es más importante saber los atributos que utilizamos en las descripción que el nombre que le damos al conjunto -o variable. Por ejemplo, si nos referimos a la variable raza, no es posible saber de antemano cuáles sonlos atributos a los que nos referiremos. Si hablamos de humanos de raza blanca, negra, roja, amarilla o de bronce, existe la posibilidad de que ni siquiera estemos de acuerdo en estar hablando de algo que se llame "raza". En cambio, si partimos de los atributos, podemos estar de acuerdo en referirnos al conjunto de atributos como "color de piel".
Al describir un objeto, debemos de seleccionar las variables adecuadas. Supóngase que se tiene una variable compuesta por los atributos {1 año de edad, 2 años de edad, 3 años de edad, ... } Llamemos edad a esta variable. Entonces, puedo tomar el acta de nacimiento de una persona, de ésta comparo la diferencia en años entre su fecha de nacimiento y la fecha actual y esa diferencia me servirá para describir a esa persona como alguien con X años de edad (uno de los atributos del conjunto). A este procedimiento se le llama medición. Podemos referirnos a esa persona también como alguien de cabello castaño, negro, blanco, amarillo, etcétera; Sin embargo, usualmente se asigna un código en el cual cada atributo se representa con un numeral. Valores como edad, estatura, peso o tiempo generalmente ya son obtenidos como numerales. En este ejemplo de color del cabello es necesario definirlo de común acuerdo en un grupo de colegas para que todos estemos al corriente de a qué nos estamos refiriendo, por ejemplo
|
Ahora, si decimos que tal persona tiene un color de cabello 5, todos sabremos que se trata de una persona pelirroja. Si otra persona tiene color de cabello 1 quizá sea algun joven rebelde con el cabello naranja, o algo por el estilo.Este procedimiento es muy común en la actualidad y tiene como objeto la economía en espacio al conservar una cantidad considerable de información en poco espacio, además de que resulta menos susceptible de error al capturar la información y más fácil de verificarla en caso necesario.
De este modo podemos definir a la medición como el procedimiento de asignar numerales a objetos de acuerdo con ciertas reglas. En este procedimiento, primero seleccionamos aquellos atributos que son relevantes para describir a nuestro objeto de estudio (podemos referirnos a ellos con algún nombre que no necesariamente debe ser una sóla palabra), observamos a nuestro objeto de estudio para determinar cuál de los atributos disponibles está presente es este objeto, consultamos cuál es el código que le corresponde al atributo encontrado en el sujeto y ¡Ya está!. En adelante ese objeto será representado en ese contexto por el numeral que corresponde a ese atributo. Ese numeral, producto del procedimiento de medición se denomina dato, y en estadística aplicada constituye la unidad de análisis básica.
Cabe aclarar qué es un numeral. Un numeral es una cadena de los símbolos que se utilizan para construir representaciones de números; por ejemplo "654" o "547.7". Debe recordarse que en este contexto el numeral se refiere a un atributo que posee el objeto y por lo tanto no tiene propiedades numéricas sino solamente en la medida en que tal atributo posea propiedades cuantitativas.
Aquí tenemos un ejemplo secillo de medición. Por un lado existe un conjunto de atributos ejemplificados con imágenes: árbol, casa, luna. reloj, gato y estrella. Por otro lado está un conjunto de numerales: 1, 2, 3, 4, 5 y 6. La regla que se aplica en este caso es que al árbol le corresponde el numeral 1, al gato el 4, a la casa el 3, a la luna el 2, al reloj el 5 y a la estrella el 6. De esta manera se cumple la definición dada anteriormente.

Para aplicar la definición dada anteriormente, ¿Qué numeral asignaría a este objeto?
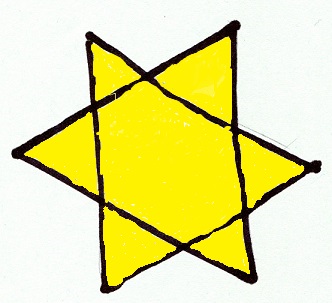
En este caso se puede considerar que le toca el numeral 6 por ser estrella, sin embargo hay que tomar en cuenta que la estrella del primer conjunto tiene cinco picos, mientras que esta nueva estrella tiene seis. La regla de asignación debe definir de manera clara las posibles variedades en que se puede presentar un objeto y cuáles de estas son válidas para aplicar correctamente la regla.
De lo anterior podemos ver dos características básicas que deben tener las categorías establecidas para cada atributo según nuestras reglas de medición. En primer lugar, la definición debe ser lo suficientemente amplia para poder identificar a todos los integrantes de esa categoría -por ejemplo, todos los gatos, todas las lunas, todos los árboles, etcétera- a pesar de las diferencias pudiera haber entre los individuos que pertenecen a la misma categoría. En segundo lugar, las definiciones de las diferentes categorías deben impedir que dos objetos que pertenezcan a diferentes categorías puedan recibir el mismo numeral, como podrìa ser el caso de una casa en un árbol.
Cumpliendo estas dos condiciones, podemos asignar el mismo numeral para identificar a dos objetos de la misma manera si poseen el mismo atributo de la dimensión a la que nos estamos refiriendo o diferentes numerales si ambos objetos poseen diferentes atributos de esa dimensión. Sin embargo, esos numerales no forzozamente tienen propiedades numéricas. Cuando nuestra medición solamente tiene estas características, los numerales usados no tienen mayor utilidad que nombrar a los objetos de acuerdo con el atributo que está presente en ellos, y corresponde a un nivel de medición nominal.
En el caso de las mediciones en un nivel nominal el orden en que pongamos a los objetos es arbitrario y por lo tanto es irrelevante. Lo mismo da colocar en primer lugar la casa y al último el reloj, que poner en primer lugar al gato y en último lugar a la luna. Por otro lado debe recordarse que los numerales representan los atributos que representan, por lo tanto aun cuando la suma 2 + 3 = 5 es correcta, en este contexto resultaría absurdo suponer que sumar una luna con una casa nos daría como resultado un reloj -con el minutero chueco, para acabarla de amolar.
En conclusión cuando una variable alcanza solamente el nivel de medición nominal no son válidas las operaciones de ordenamiento ni las operaciones aritméticas.
|
Si el atributo que estamos registrando permite ordenar objetos de acuerdo con el grado en que poseen dicho atributo, entonces podemos asignar los numerales de manera que a mayor grado corresponda un numeral mayor, o de modo que a mayor grado corresponda un numeral menor, según nuestra elección. En este caso, hemos alcanzado el nivel de medición ordinal y los numerales tienen la propiedad de orden, por ejemplo, si estamos registrando el grado que tiene un grupo de individuos pertenecientes a una corporación militar, podríamos tener los valores que se muestran en la siguiente tabla.
La primera culumna para cada categoría cuál es el rango correspondiente. El rango en este contexto corresponde a la posición que ocupa un valor en una serie de valores ordenados. así, el valor "teniente" tiene el rango 4, mientras que el rango 7 corresponde al valor "coronel".
Debe notarse que es posible identificar en cualquier lugar -una cantina, el dormitorio, etcétera- a todos los coroneles, soldados o cabos presentes. Esto significa que al hablar del nivel ordinal de medición no estamos hablando de un tipo de medición diferente, sino de una medición más elaborada. En un nivel ordinal no solamente podemos diferenciar entre objetos, sino que también es posible ordenarlos en cuanto a alguna medida de del grado en que los objetos poseen la propiedad que se está midiendo.
En el caso de una variable que se encuentra en un nivel ordinal, es válido ordenar los valores tanto de mayor a menor como ordenarlos de menor a mayor -como se observa en el ejemplo. El orden nos indica cuál de dos objetos tiene en mayor medida una propiedad que cuál otro -en este ejemplo, autoridad o mando. Pero no es posible indicar con precisión cuál es la magnitud de la diferencia. Es por esta razón que aquí tampoco son válidas las operaciones aritméticas: aun cuando 2 + 5 = 7, resultará absurdo suponer que al sumar la autoridad de un cabo con la de un capitán tendríamos la autoridad de un coronel. Deber recordarse siempre que las operaciones las estamos realizando con los atributos que representan los numerales y no con los numerales como representación de números.
El nivel de medición por intervalos es una medición más elaborada en la cual se dispone de una unidad de medida que nos permite no solamente indicar que un objeto posee un mayor grado de una propiedad que otro, sino que permite indicar la magnitud de esa diferencia. Un ejemplo muy sencillo lo representa la variable estatura. En este ejemplo vamos a definir la estatura como la altura del plano sagital de una persona y para representar esta medida utilizaremos una escala expresada en centímetros. Para ejemplificarlo pediremos ayuda a los seis hijos de la familia Ibargüengoitia: Jacinto, Aureliano, Rigoberto, Esculapio, Epifanio y fortunato, quienes aparecen en la siguiente figura:
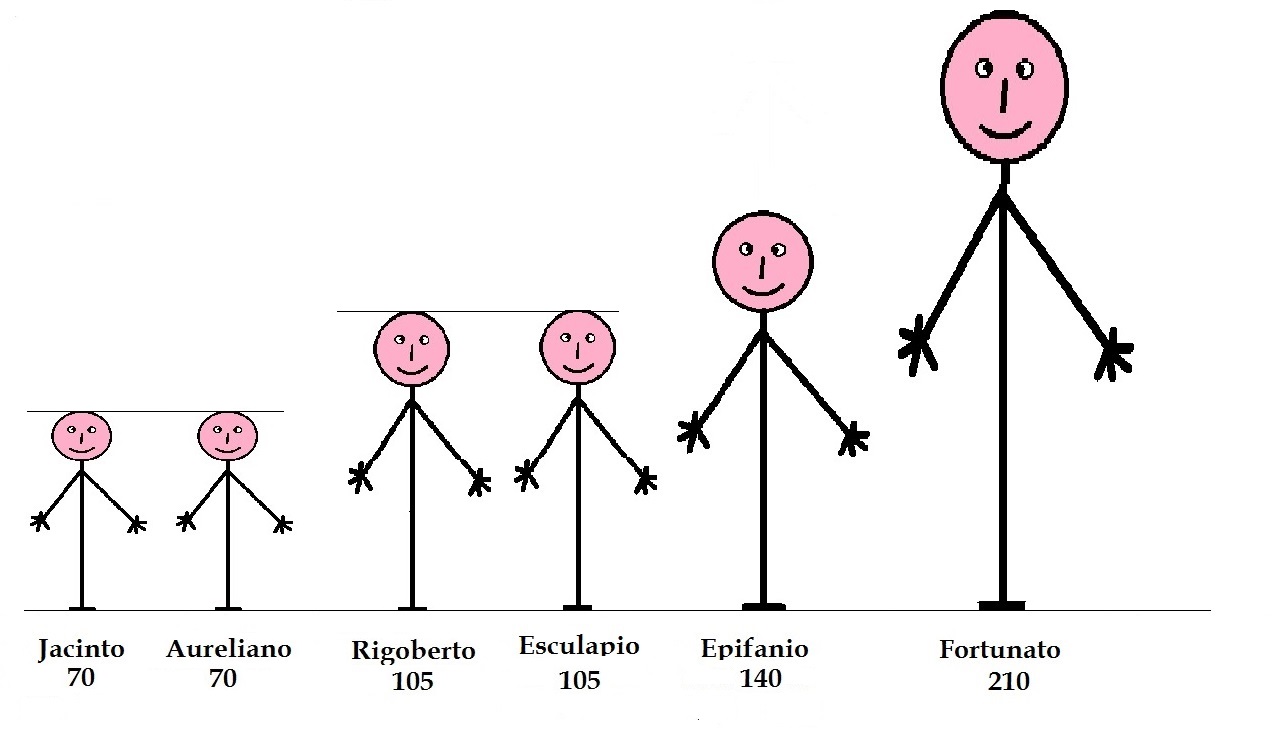
Debajo de cada imagen aparecen el nombre y la estatura de cada quien. Como puede observarse en la imagen, Jacinto y Aureliano tienen la misma estatura, así como Rigoberto y Esculapio, lo cual significa que nuestra medición tiene la propiedad nominal que nos permite determinar si dos objetos son iguales y diferentes.
Además de esto, los niños están bien educados y a la hora de presentarse se forman de menor a mayor -y podemos ver si están formados correctamente o no-, lo que nos dice que en esta variable está presente la propiedad ordinal.
Finalmente tenemos otra propiedad muy importante que se muestra en la siguiente figura:
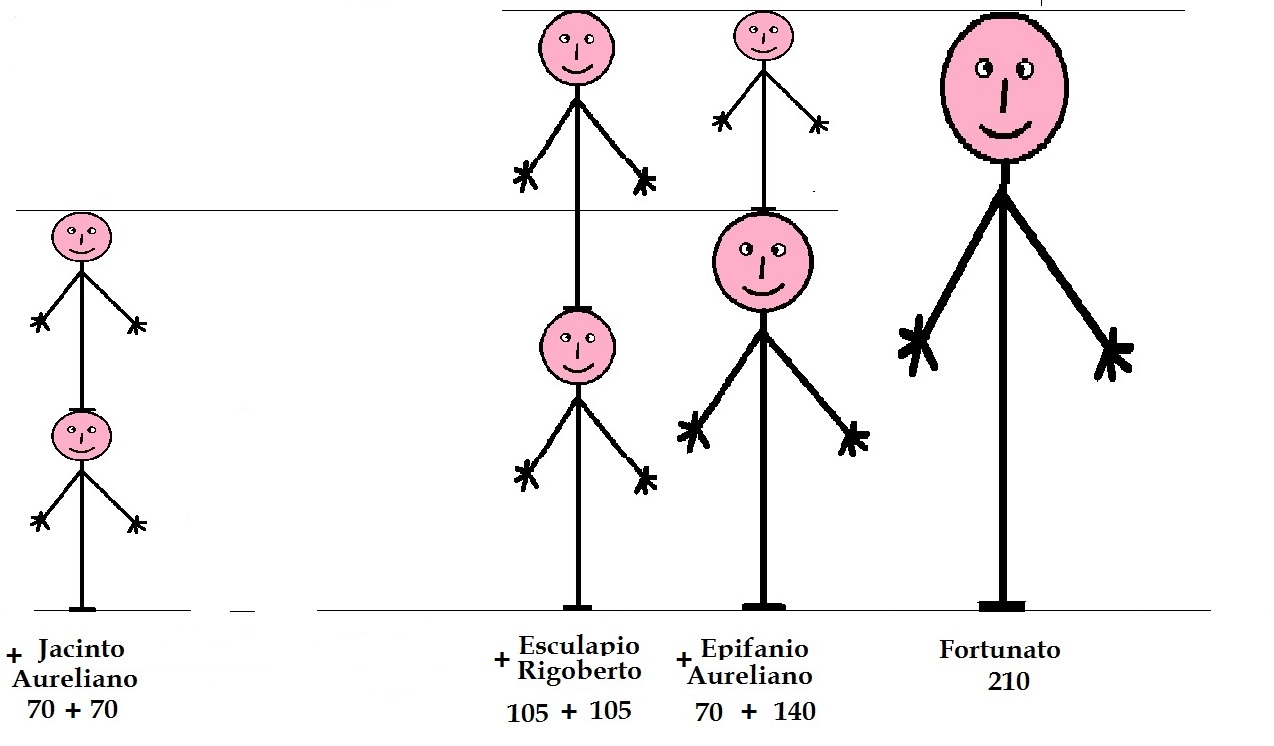
Si sumamos la estatura de Epifanio con la de Aureliano tendremos la estatura de fortunato (1). Si sumamos la estatura de Esculapio con la de Rigoberto, también obtenemos la altura de Fortunato (2). Si sumamos la estatura de Jacinto con la de Aureliano, obtendremos la estatura de Epifanio (3), como se observa en la imagen. Si no realizamos estas operaciones con la propiedad que poseen estos niños, sino con los valores obtenidos en nuestra escala (centímetros), obtenemos los mismos resultados: 70 + 140 = 210 (1); 105 + 105 = 210 (2); y 70 + 70 = 140 (3). La diferencia de estatura entre Fortunato y Epifanio es igual a la estatura de Aureliano; La diferencia de estatura entre Epifanio y Jacinto es igual a la estatura de Aureliano. Expresado en números, la diferencia entre 210 y 140 es 70, y la diferencia entre 140 y 70 es 70. Expresado de una manera más formal: Si a iguales intervalos entre las propiedades (estatura) de los objetos corresponden iguales intervalos en nuestra escala (centímetros), esto significa que tenemos una unidad estándar de medida y esta característica es lo que define al nivel de medición de intervalos.
En el nivel de medición de intervalos, al disponer de una unidad de medida, ya es válido realizar operaciones de adición y por lo tanto, también de sustracción, multiplicación y división que son operaciones comunes en estadística. Debe anotarse que el nivel de medición no depende únicamente de la propiedad que se mide en los objetos, sino que es muy importante la definición de nuestra variable, la cual incluye los valores de la escala que se utilice y las reglas de asignación de estos numerales a los objetos que se están midiendo.