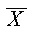
El análisis de varianza es un modelo que permite decidir si ha de suponerse que una o más variables independientes están relacionadas con una variable dependiente. Supóngase que queremos examinar la suposición de que la actitud del profesor -(A)utoritario, (D)emocrático o (P)ermisivo) está relacionado con el aprovechamiento escolar en la materia de Estadística. Supóngase también que disponemos de un instrumento que permite medir el aprovechamiento escolar en un nivel de medición de intervalos.
Después de entrenar a tres profesores para que puedan mostrar ante los estudiantes cada una de estas actitudes, seleccionaremos a una muestra de estudiantes y la dividiremos en tres muestras -de preferencia del mismo tamaño. Después, cada uno de estos grupos sufrirá o disfrutará el curso dependiendo de si en su grupo el profesor muestra una actitud autoritaria, democrática o permisiva, respectivamente.
Si ambas variables están relacionadas, entonces al terminar el curso los grupos tendrán diferentes promedios de aprovechamiento. También se esperaría que cada promedio reflejara una tendencia común en las puntuaciones de cada grupo. Esto significa también que las diferencias entre los promedios de los grupos debería ser mayor que las diferencias que se encuentran entre los individuos que conforman los grupos.
Si comparamos dos grupos tendremos una diferencia, en cuyo caso la podemos evaluar utilizando una prueba t de Student. Podemos también hacerlo con un análisis de varianza, en cuyo caso obtendremos el mismo valor de significancia. Si comparamos más de dos grupos tendremos, obviamente, tres o más diferencias. En efecto, si se tienen J grupos, el número de diferencias será el factorial de (J-1). En este caso, la probabilidad de obtener una diferencia grande por efecto del azar (o del error de muestreo) aumenta, haciendo que una evaluación de las diferencias una a una sea incorrecto.
Una manera más conveniente de evaluar un conjunto de diferencias es a través de la varianza, que es un promedio de diferencias elevadas al cuadrado. El modelo que se sigue es el siguiente. En la Tabla 1 se muestra el esquema del problema planteado al principio: se tienen tres grupos de estudiantes y las puntuaciones de cada grupo -inventadas- se muestran en columnas encabezadas por el valor de la variable independiente Actitud del profesor que se aplica a ese grupo; al pie de cada columna se muestra la media aritmética de cada grupo.
| Autoritario | Democrático | Permisivo | |
| 12 | 14 | 18 | |
| 13 | 13 | 19 | |
| 15 | 16 | 21 | |
| 14 | 17 | 14 | |
| 11 | 14 | 23 | |
| 15 | 15 | 19 | |
| 16 | 16 | 23 | |
| 13 | 13 | 18 | |
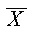 | 13.625 | 14.75 | 19.375 |
En esta tabla podemos ver la varianza -variabilidad- que hay en los datos. Esta varianza la podemos clasificar de acuerdo de la fuente de la que procede.
En primer lugar tenemos las diferencias que se observan entre todas las puntuaciones y a esta la vamos a llamar varianza total.
En segundo lugar, se tiene las diferencias que hay entre las medias de los grupos. la explicación de las diferencias entre las medias es que los grupos están sometidos a diferentes valores de la variable independiente -actitud del profesor- y esto va a producir cambios sistemáticos en el valor de la variable dependiente -aprovechamiento escolar. A esta varianza la vamos a llamar varianza sistemática, varianza explicada o, simplemente, varianza entre grupos. Finalmente, si se supone que los estudiantes eran similares en cuanto a aprovechamiento, no hay modo de explicar las diferencias que hay entre las puntuaciones de los estudiantes del mismo grupo. A esta varianza se le llama varianza no explicada, varianza de error -producida por el error de muestreo- o, simplemente, varianza intragrupo.
Para considerar que las diferencias entre grupos son indicio de una relación entre nuestras variables, esto es que las diferencias son significativas, la varianza explicada debe ser grande en comparación con la varianza no explicada. Esto se expresa como una razón, o proporción F cuya significancia se obtiene de la tabla de la distribución de probabilidades de Fisher.
El modelo delineado arriba es el más simple. Hay algunos cambios en el modelo dependiendo del diseño específico utilizado.
Gráficamente, el modelo se puede representar de la siguiente manera:
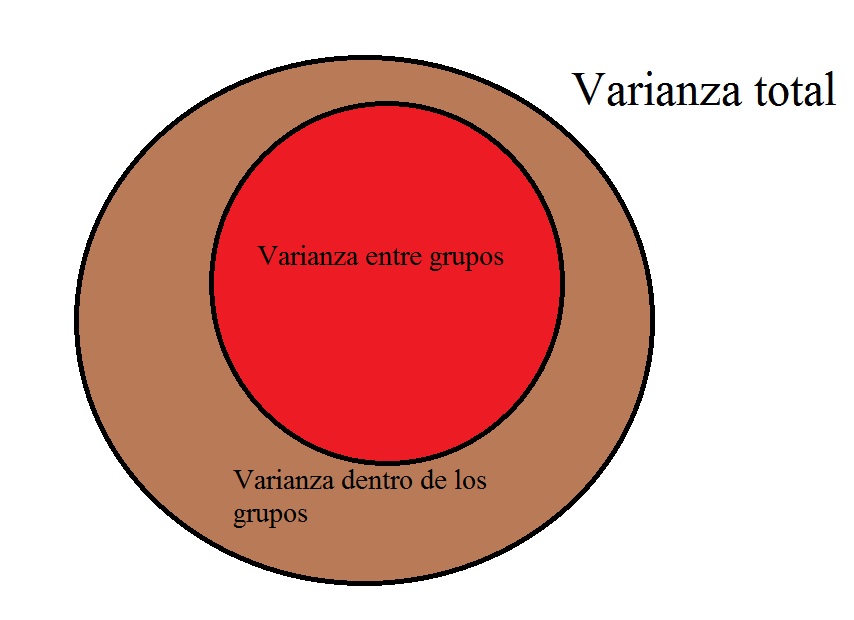
El círculo mayor representa toda la varianza contenida en el diseño. Una parte de la varianza es explicada por la relación que existe entre ambas variables y se muestra en color rojo. El color café muestra la varianza que no se puede explicar, o varianza de error.
Recordando la fórmula de la varianza:

Para que la varianza de la muestra haga una mejor estimación de la varianza poblacional, se cambia el denominador por los grados de libertad (gl) dividiendo no por n sino por n-1. Dependiendo de la fuente de varianza, puede cambiar el cálculo de los grados de libertad, como veremos más adelante. Así tendremos la fórmula:
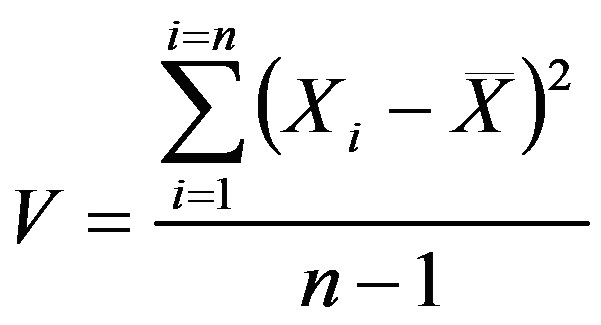
En el numerador de la fórmula tenemos la suma de diferencias de las puntuaciones con respecto a la media elevadas al cuadrado, y se le denomina suma de cuadrados, o SC. Así que en breve tenemos la fórmula final:
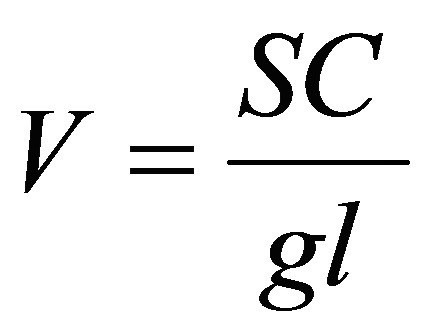
Entonces, para hacer un análisis de varianza con una variable deben calcularse, para cada fuente de varianza, las sumas de cuadrados, los grados de libertad y luego dividir SC/gl, con lo que se obtiene la varianza, que en este contexto se denomina media de los cuadrados o MC. Finalmente se divide la varianza entre grupos por la varianza dentro de los grupos para obtener la razón F de fisher. Estos cálculos intermedios se presentan en una tabla de resumen de análisis de varianza como la que se muestra abajo
| Fuente | SC | gl | MC | F |
| Entre | 148.58 | 2 | 74.29 | 16.04 |
| Dentro | 97.25 | 21 | 4.63 | |
| Total | 245.83 | 23 |
En esta tabla se pueden observar algunas particularidades. Como se deprende del modelo, la suma de cuadrados entre grupos (sce) más la suma de cuadrados dentro de los grupos (scd) coincide con la suma de cuadrados total y los grados de libertad entre grupos (gle) más los grados de libertad dentro de los grupos (GLD) es igual a los grados de libertad totales. La suma de las medias de cuadrados entre grupos y dentro de los grupos no coincide con la media de los cuadrados, de modo que esa casilla en la columna 3 de la tabla se deja vacía, y la razón F se calcula solamente considerando las fuentes de varianza entre grupos. Estas características son útiles al verificar los pasos en nuestros cálculos. Deberíamos agregar que, al tratarse de varianzas, ningún valor en la tabla debe ser negativo.
Al calcular el valor F, dividimos la media de los cuadrados entre (MCE) por la media de los cuadrados dentro (MCD). Para obtener MCE dividimos la suma de los cuadrados entre (MCE) por los grados de libertad entre (gle); Por lo tanto, gle están asociados al numerador de la fórmula de F. Del mismo modo, para obtener MCD se divide SCD por gld, de modo que gld están asociados al denominador de la fórmula de F. Con estos grados de libertad se consulta la tabla de la distribución de probabilidades de la distribución F de Fisher.
En la tabla de la distribución F se identifican en la primera fila los grados de libertad asociados al numerador, esto es, gle; también se identifica los grados de libertad asociados al denominador, gld rotulando las filas. Para cada combinación se muestran tres columnas para los percentiles 95, 99 y 99.9 de esta distribución. En el ejemplo que nos ocupa se tienen dos grados de libertad para el numerador y 21 grados de libertad para el denominador; para que nuestro resultado tenga una significancia de .05 la razón F debe tener un valor igual o superior a 3.4668, para que tenga una significancia de 0.01 debe ser igual o mayor a 5.7804 y para que sea significativo al nivel de .001 el valor de F debe ser igual o mayor que 9.7723. En nuestro ejemplo, nuestra F tiene un valor de 16.04 y por lo tanto es significativo al nivel de .001.
Análisis de Varianza para un diseño factorial.
La explicación anterior puede ampliarse con pocos cambios a un diseño en el cual se manejen más de una variable independiente y una variable dependiente. Suponga que se desea investigar el efecto que tienen la modalidad de privación -de agua o comida- y la raza -whistar o Long evans- en ratas sobre la velocidad de recorrido de un laberinto. El diseño necesario para realizar esta investigación incluirá un grupo para cada combinación de un valor de una variable con cada valor de la segunda variable. A continuación se muestran datos ficticios mostrando dos tipos de organización que se pueden encontrar en textos de la materia: el primero no es muy común, pero su presentación es más económica en términos de espacio vertical en un texto impreso:
| Agua | Alimento | ||
| Whistar | Long e. | Whistar | Long e. |
| 20 | 26 | 20 | 25 |
| 22 | 26 | 24 | 22 |
| 24 | 29 | 18 | 20 |
| 15 | 24 | 19 | 20 |
| 22 | 25 | 22 | 26 |
| 19 | 24 | 22 | 23 |
| 16 | 24 | 26 | 17 |
| 17 | 28 | 24 | 20 |
| 16 | 27 | 26 | 20 |
| 22 | 21 | 27 | 24 |
En la siguiente tabla se muestran los mismos datos con una organización que permite mostrar en columnas los datos asociados a cada uno de los valores de una variable independiente, y en filas los datos asociados a cada uno de los valores de la otra variable independiente, haciendo más fácil la identificación de los datos del diseño.
| Whistar | Long e. | |
| Agua | 20 | 26 |
| 22 | 26 | |
| 24 | 29 | |
| 15 | 24 | |
| 22 | 25 | |
| 19 | 24 | |
| 16 | 24 | |
| 17 | 28 | |
| 16 | 27 | |
| 22 | 21 | |
| Alimento | 20 | 25 |
| 24 | 22 | |
| 18 | 20 | |
| 19 | 20 | |
| 22 | 26 | |
| 22 | 23 | |
| 26 | 17 | |
| 24 | 20 | |
| 26 | 20 | |
| 27 | 24 |
El modelo para este diseño puede verse en la siguiente figura:
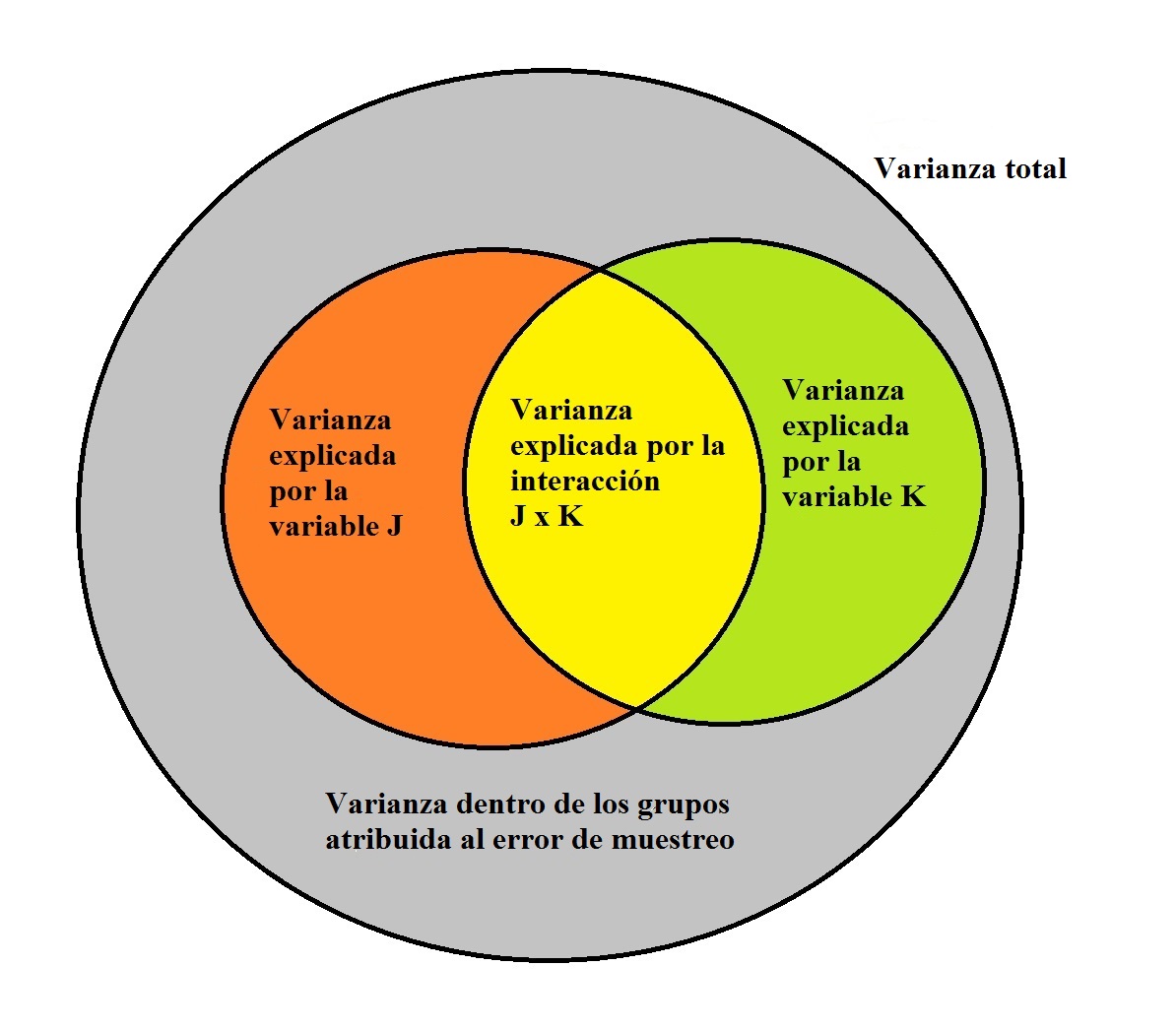
En este caso, la varianza total comprende la varianza que puede ser explicada por la variable independiente J, y la varianza explicada por la variable independiente K, a las que llamaremos varianza debida a los efectos principales.
Además, una parte de la varianza total no siempre puede explicarse por el efecto que tienen las variables independientes por sí solas, y tiene que explicarse por el efecto conjunto de ambas variables. A esta varianza se le denomina varianza debida a la interacción entre las variables independientes. Esta varianza indica el grado en que el efecto que tiene una variable independiente puede ser modificado por el valor de otra variable independiente. Por ejemplo, la velocidad del recorrido puede ser menor cuando el sujeto está privado de agua que cuando es privado de alimento si el sujeto es de la raza whistar, pero en el caso de los sujetos long evans la velocidad del recorrido puede ser menor cuando está privado de alimento que cuando está privado de agua. Es este ejemplo, hay una interacción entre la raza del sujeto y el tipo de privación a que está sometido.
Para ilustrar este ejemplo, a continuación se presentan unos resultados ficticios. En primer lugar, de la inspección de la figura anterior, se pueden identificar las fuentes de varianza total, varianza explicada (entre grupos) y varianza no explicada (dentro de los grupos). A su vez, la varianza entre grupos se descompone en la varianza explicada por la primera variable independiente y la varianza explicada por la segunda variable independiente (varianza debida a efectos principales), y la varianza debida a la interacción entre ambas variables independientes. Estas fuentes de varianza y sus valores respectivos se presentan a continuación.
| Fuente | SC | gl | MC | F | p |
| Entre Raza | 62.5 | 1 | 62.5 | 7.5962 | 0.0091 |
| Entre Privacion | 0.1 | 1 | 0.1 | 0.0122 | 0.9127 |
| Int R x P | 129.6 | 1 | 129.6 | 15.7515 | 0.0003 |
| Entre Total | 192.2 | 3 | 64.0667 | 7.7866 | |
| Dentro | 296.2 | 36 | 8.2278 | ||
| Total | 488.4 | 39 |
Al analizar esta tabla podemos notar que la suma de las sumas de cuadrados entre total y dentro de los grupos coincide con la suma de cuadrados total, y que la suma de las sumas de cuadrados debidas a los efectos principales más la suma de cuadrados debida a la interacción entre las variables independientes es igual a la suma de cuadrados entre total. La misma coincidencia se encuentra entre los valores de los grados de libertad.
Con respecto a lo que muestra la tabla, se puede observar que es significativa la varianza debida a la varable raza, así como la varianza debida a la interacción entre la variable raza y la variable privación. Para entender a qué se refiere este análisis y para poder describir con más detalle los resultados, es necesario revisar las medias incluidas en el diseño, como se muestra en la siguiente tabla
| Whistar | Long evans | Medias privación | |
| Agua | 19.3 | 25.4 | 22.35 |
| Alimento | 22.8 | 21.7 | 22.25 |
| Medias raza | 21.05 | 23.55 |
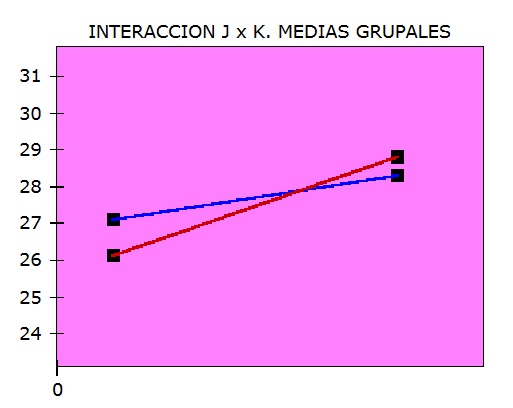
En esta tabla se puede ver que la diferencia entre la velocidad de recorrido de las ratas Long evans es significativamente mayor que la de las ratas Whistar (25.55 Vs. 21.05) mientras que la diferencia entre las condiciones de privación no lo es (22.35 Vs. 22.25), de acuerdo con la tabla de análisis de varianza. Sin embargo, la interpretación de la diferencia de velocidad entre razas debe interpretarse tomando en cuenta la interacción entre ambas variables, dado que el efecto de la raza varía según el tipo de privación de los sujetos. La interacción puede visualizarse si se grafican las medias grupales como en la gráfica que aparece abajo. La velocidad de las ratas Whistar es mayor que las Long Evans si están privadas de alimento, mientras que las Long evans son más veloces si están sometidas a privación de agua
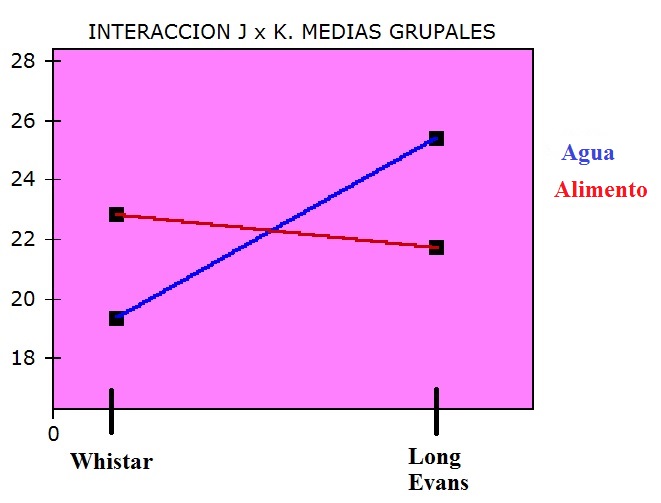
Es así como el análisis de varianza muestra su utilidad para desentrañar las relaciones entre variables cuando se manipulan dos o más variables independientes simultáneamente permitiendo no solamente aislar el efecto de cada variable sobre la variable dependiente, sino proporcionando también información sobre las relaciones que pueden existir entre las variables independientes.
En este caso, se ha escrito sobre la lógica de la aplicación del análisis de varianza cuando se utiliza un diseño de grupos al azar.Si se emplea un disño de muestras relacionadas es posible identificar una variaza debida a las diferencias que hay entre los sujetos. El modelo en este caso indica que esta varianza no interactúa con el efecto producido por las variables independientes y se debe agregar a los modelos anteriores como una fuente más de varianza. Abajo se muestran gráficamente los cambios que hay en los modelos de análisis de varianza y los cambios correspondientes en las tablas de resumen de análisis de varianza. Para cada caso se muestra los dos análisis de varianza sobre el mismo conjunto de datos: uno suponiendo que el dise�o es completamente al azar y el otro suponiendo que se utiliza un dise�o de bloques al azar.
| Análisis de varianza simple | Análsisis de varianza factorial J x K | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|

|

|
En la tabla anterior se comparan los resultados del análisis de varianza para modelos al azar y de muestras relacionadas o de bloques al azar, como también se le conoce. Dos puntos hay que resaltar. Por un lado, no cambian los valores para las sumas de cuadrados correspondientes a los efectos principales -ni a la interacción en el análisis factorial. Lo único que ocurres es que la suma de cuadrados se resta de la suma de cuadrados correspondiente al error de muestreo. Esto es así porque se puede indentificar una fuente de varianza más, que es la que se debe a las diferencias entre los sujetos que componen la muestra. El otro punto, que es consecuencia del anterior, es que la proporción F aumenta para las fuentes de varianza sistemática al reducirse el valor de la Media de los Cuadrados dentro de los grupos, que es usada como denominador en la proporción F.
Si se observa la gráfica de las medias para observar la interacción, puede notarse también que éstas relaciones no son modificadas. En efecto, lo único que cambia es la significancia de los efectos, y no los efectos en sí.
Sin embargo, hay que tomar en cuenta que este efecto -aumentar la probabilidad de que F sea significativa- no está garantizado pues depende de que la variable que se use para aparear los grupos esté relacionada de manera efectiva con la variable dependiente, pues en otro caso, el aparear estos grupos tendrá poca influencia sobre los valores de F, pues el efecto de dicha variable sería más bien aleatorio y la varianza debida a las diferencias individuales sería mínima.
En las siguientes páginas se procederá a mostrar los procedimientos para realizar estas modalidades del Análisis de Varianza.